I. Bevezető a gráfokról
A Mindentudás Egyetemének sok előadása foglalkozott már hálózatokkal (matematikai nevükön gráfokkal). A legutóbbi két előadásban Vicsek Tamás és Kertész János a tudomány, technika és társadalom legkülönbözőbb területein megtalálható hálózatokat vizsgálta. Itt az ideje, hogy a matematikus szemével, általánosan is megnézzük ezeket a nagy hálózatokat.
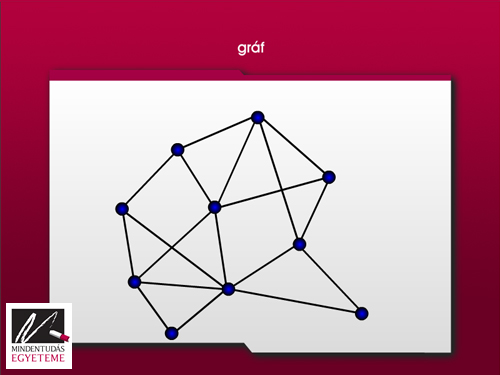
Első ábránkat akár egy gráfelméleti tankönyvből is vehetnénk. Egy gráf csúcsokból és a csúcsokat összekötő élekből áll. Egy csúcs fokának (fokszámának) nevezzük a belőle kiinduló élek számát. Annak illusztrálására, hogy milyen jellegű kérdéseket lehet vizsgálni egy ilyen gráffal kapcsolatban, említsünk meg egyet: mikor lehet egy gráfot egyetlen vonallal úgy lerajzolni, hogy minden élen pontosan egyszer haladunk át? Ezt a – talán legklasszikusabb – gráfelméleti kérdést a königsbergi hidak problémájának nevezik, és Euler oldotta meg több mint 250 évvel ezelőtt.
Az 1. ábrán látható gráfot például nem lehet így lerajzolni. Ehhez nézzük azt a csúcsot, melyből 5 él indul ki. Valahányszor áthaladunk a csúcson, két élt használunk el (t.i. egyet a beérkezéshez és egy másikat a továbbhaladáshoz), és mivel az 5 páratlan szám, ezért vagy ebből a csúcsból kell indulnunk, vagy a végén ide kell megérkeznünk. De ugyanez minden páratlan fokú csúcsról elmondható, és ilyen csúcsból négy is van. Tegyük fel, hogy az egyikből indulunk, a másikban végzünk, de még mindig marad két páratlan fokszámú csúcs, amelyekből kiinduló éleket nem tudjuk mind megrajzolni.
A 2. ábra olyan gráfot mutat, melynek 100 csúcsa van. Ez a mérete alapján lehetne mondjuk egy kisebbfajta beruházás kivitelézési hálója. Ekkora gráfot a rajz alapján már nehéz áttekinteni, de számítógépekkel könnyen kezelhető.

A 3. ábra gráfja már egészen ijesztő, bár csak 3000 csúcsa van. Ezt már szemmel egyáltalában nem látjuk át, de számítógéppel még sok fontos tulajdonsága meghatározható. Mi ez azonban az internethez képest?

II. Nagyon nagy gráfok
A 4. ábra két próbálkozást mutat az internet ábrázolására. Szépek, de meg kell jegyeznem, hogy nekem nem sokat mondanak. Sok más nagy hálózat van, amit szeretnénk megérteni. Ilyenek például a legkülönbözőbb társadalmi hálózatok: nem csak az iwiw, de az emberek közötti ismeretségek gráfja, rokonságok gráfja stb, melyeknek több mint hatmilliárd csúcsa van. Más jellegű nagyon nagy hálózatok az integrált áramkörök (chip-ek).

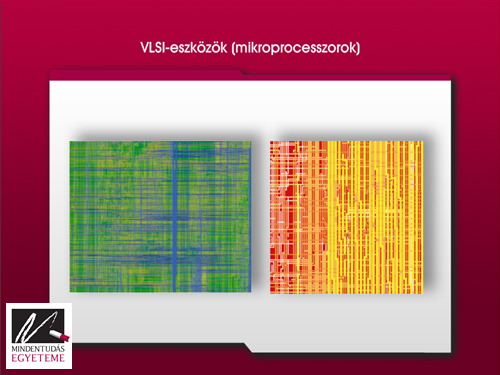
Az 5. ábra csak két kis részletét mutatja egy modern integrált áramkörnek, mely százmilliónyi elemből áll. Bár ezek minden részletükben tervezettek, lerajzolásuk és megértésük nehéz, mert rendkívül hatalmasak.
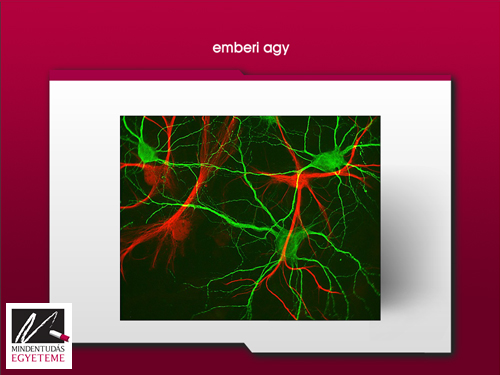
Az agy százmilliárdnyi csúcsú gráfja talán a legizgalmasabb mind között, de sajnos keveset tudunk róla gráfelméleti szempontból.
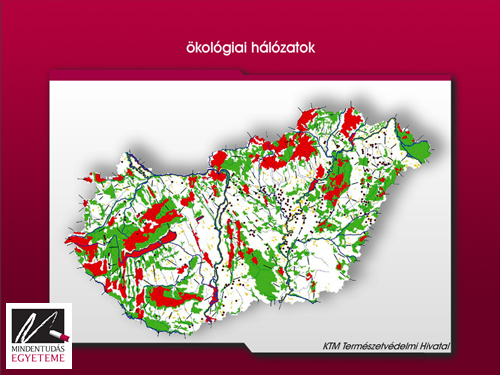
Hatalmas méretű, bonyolult hálózatokat alkotnak az ökológiai rendszerek. A 7. ábra alapján különböző térségek közötti kölcsönhatásokat modellezhetünk, de lejjebb is mehetünk a fajok, sőt, az egyedek szintjére.
A fizika is szolgáltat néhány nagyon izgalmas hálózatot: talán az egész Világegyetem egyetlen nagy hálózat, mely elemi részekből és az azok közötti kölcsönhatásokból áll. De erről nemigen tudok mit mondani, így inkább egy sokkal egyszerűbb struktúráról fogok néhány szót szólni: a kristályszerkezetről (8. ábra).

Egy fémdarab atomokból és azok közötti kötésekből áll. Egy tökéletes kristály gráfja iszonyú sok, mondjuk 1030 csúcsból áll, bár eléggé unalmas, mondjuk egy kocka ismétlődik nagyon sokszor. A valóságban minden kristályban vannak szabálytalanságok (szennyeződések, törésvonalak, hiányok, stb.), amitől érdekessé válik. A kristályos anyagot azonban nem mindig célszerű gráfként elképzelni vagy leírni: a mérnök a kristályt folytonos anyagnak tekinti, melynek fontos tulajdonságait (pl. rugalmasság, nyúlás, rezgések) a matematika eszközeivel, differenciálegyenletekkel írja le. Ugyanakkor más tulajdonságok, mint pl. a mágnesezhetőség vagy az olvadáspont csak az atomos leírásból érthetők meg. Egyebek mellett ezekkel a kérdésekkel foglalkozik a statisztikus fizika. E problémák megoldása gyakran számítógépes szimuláció segítségével történik, amelyben ugyanolyan kristályszerkezetű, de sokkal kisebb, néhány száz vagy ezer atomból álló, idealizált kristályt használnak. Tehát a 1030 atomból álló valódi kristályt kétféleképpen is közelíthetjük: végtelen, folytonos struktúrával illetve sokkal kevesebb atomból álló idealizált kristállymodellel. De vajon lehet-e ilyen közelítéseket keresni más, hasonlóan gigantikus méretű hálózatok esetén is?
Mielőtt a kérdés tárgyalásába kezdenénk, gondoljuk végig, hogy mit is akarunk vizsgálni egy nagyon nagy hálózattal, pl. az internettel kapcsolatban. Nézzünk néhány konkrét kérdést, amit kis gráfokkal kapcsolatban lépten-nyomon felteszünk:
- Páros vagy páratlan számú csúcsa van-e az internetnek?
Ez a kérdés a klasszikus gráfelméletben sokszor előjön, de az internetre vonatkozóan nyilvánvalóan értelmetlen, hiszen egyrészt az internet pillanatról pillanatra változik, másrészt nem világos, hogy hova sorolhatók azok a számítógépek, amelyeket éppen ki- vagy bekapcsolnak.
- Hány éle van az internetnek?
Persze a pontos számra rákérdezni értelmetlenség. Ugyanakkor, ha nem a pontos válasz az érdekes, hanem megengedünk pl. 1%-os pontatlanságot, akkor már értelmes a kérdés.
- Összefüggő-e az internet?
Erre a válasz biztosan az, hogy nem, hiszen valahol egy router biztosan el van romolva, ezáltal néhány boldogtalan felhasználó mindig el van vágva a többitől. A kérdés azonban nem egészen erre irányult, inkább arra, hogy nem esik-e szét az internet két (vagy több), az egésszel összemérhető nagyságú részre. Néhány hete például egy hajó elvágta az Európa és Afrika közötti tengeralatti kábelt és egy időre Afrika egyes részeivel minden kapcsolat megszakadt… Látjuk tehát, hogy ilyen nagyméretű hálózatok esetén a klasszikus kérdések egy része értelmetlen, más részüket pedig módosítani kell ahhoz, hogy érdekesek, relevánsak legyenek.
Az előadás folytatása itt olvasható.

Kommentek
Kommenteléshez kérlek, jelentkezz be: