Jakabffy Éva, IPM, 2008. december
Legtöbbünk számára a matematika csak az iskolában központi kérdés, másutt a peremre szorul, mint egy való élettől elrugaszkodott, az alapszinten túl felfoghatatlanul elvont tudomány. Építményének magasságait inkább csodáljuk, mint szeretjük, s a felsőbb emeletek lakóit misztikus lényeknek érezzük, mivel nem osztozunk gondolataikban. Van-e egyáltalán szilárd talaja e matematikai építménynek, vagy csak lebeg a semmiben? És főleg, jó-e egyáltalán valamire? E kételyeket talán eloszlatná, ha lelki szemeink előtt hirtelen megjelenne az az ősünk, aki először jelölte és ásta ki az építmény helyét, majd az, aki első köveit lerakta.
Mezopotámiában, Uruk egyik templomának az i. e. IV. évezredből eredő agyagtábláin már találkozunk pontos mennyiségekkel, azaz számokkal. Mi különös van ebben, kérdezhetnénk. A számok önmagukban egyszerű jószágok, pláne, hogy részint éppen jószágok – például szarvasmarhák – számontartását szolgálták. Egyesével számlálni, ez igazán nem nagy teljesítmény, gondolhatnánk. Pedig éppen ez a matematika égbe nyúló építményének alapköve. Ehhez fel kellett fedezni a számokat, mint egymástól elkülönülő „entitásokat”. Hogyan is történt mindez? Elképzelhető, hogy mint minden újítás, a számok ötlete is egy zseniális – vagy több kongeniális – agyból pattant ki. Rájöhettek, hogy ily módon „számon” lehet tartani olyan dolgokat, amilyeneket addig nem: ki mivel tartozik; ki hány tehenet adott, és ezért hány zsák búza illeti meg; vagy mikor lesznek a létfontosságú víznek bővében, mikor lesz itt az áradás vagy az esőzések ideje. Ebből aztán kialakultak a kereskedést segítő elszámolások (ilyen látható az uruki táblákon), illetve az első csillagászati naptárak is.
Egy ilyen áttekintés azonban szükségszerűen torzít; a lényeget emelve ki, lerövidíti az időt visszapillantásunk előtt. Mintha a számok – és a számokon alapuló kultúra – egyfajta emberi creatio ex nihilo (semmiből való teremtés) révén állt volna elő. Ilyen azonban csak kollektív tudattalanunkban létezik, amelynek mélyebb rétegeiben talán mindannyian ott találjuk a mitikus teremtéstörténet egy változatát. E történet egyetlen mozzanatba sűríti bele azt, ami akár évezredek-évmilliók fejlődésének eredménye. Még ha igaz is, hogy a számokat egyszer csak kitalálták, ez a pillanat már csak egy végpontja volt a mennyiségekkel kapcsolatos tapasztalatok rendkívül hosszú időn és számtalan nemzedéken át történt felhalmozódásának. Az is lehet, hogy a számfogalom több helyen is megjelent; s hogy ez mikor történt először, erre éppoly nehéz pontos választ kapni, mint dátummal ellátni az első értelmes szót, vagy megállapítani, ki volt az, aki elsőként ajánlotta kedves halottját az égiek kegyébe.
Két csont és egy végrendelet
Első látásra csak rovátkázott eszközökről van szó: olyan csontleletekről, amelyeknek nem sok közük van Pythagoras tételéhez, de még az egyszerű elszámolásokhoz sem. Mindkét leletet Ishangóban, egy a Kongói Demokratikus köztársaságbeli kis faluban, a Nílus egyik legtávolabbi forrásvidékén találta Jean de Heinzelin belga geológus. 
Az első egy 10 centiméter körüli, enyhén ívelt csont, amelynek végébe kvarcdarabot illesztettek. Egyes források szerint oroszlántól származik. Először 8500 évesre becsülték; alaposabb vizsgálat azonban kiderítette, hogy jóval régebbi. A geológiai réteg, amelyben kagylók és horgok közt megőrződött, 22 000 év körüli korra utal. Hogy a geológus egy másik csontot is talált Ishangóban, ennek tudását egyelőre az emberi indiszkréciónak köszönhetjük. Heinzelin ugyanis halálos ágyán, 1998. november 4-én adta tudtára munkatársainak, hogy még egy csontlelet van a birtokában. Megbízta őket, hogy erről készülő publikációját fejezzék be, majd posthumus jelentessék meg, de mindvégig őrizzék végrendelete titkát. Utóbbit egy újságíró megszegte, így már a második csontnak is híre ment. Eddigre azonban a tudósok már évtizedes vitákat folytattak le az első csontról. Az ezen látható rovátkák sora ugyanis már első benyomásra számolási tevékenységre emlékeztet, olyasfajtára, mint amikor függőleges, rövid vonásokat írunk, négyesével áthúzva. A vonások számokra fordíthatók, így a csonton a következő számsorokat kapjuk: 11, 21, 19, 9 11, 13, 17, 19 3, 6, 4, 8, 10, 5, 5, 7
Egy Holdon járó hipotézis
A tudósok rögtön belelátták ezekbe a maguk elképzeléseit. Nemcsak matematikusokat foglalkoztatott a rejtély. A 70-es években Alexander Marshack amerikai újságíró nem kisebb megbízást kapott a NASA-tól, mint hogy írja meg a tudományok történetét. Ő arra jutott, hogy a tudományok – amelyek utóbb elvezettek a világűr meghódításához – bizony az ishangói csonttal kezdődtek. E sok ezer éves matematikai tárgyba úgy beleszeretett, hogy autodidakta régésszé képezte ki magát, s később szép kitüntetéseket is kapott. Vésett csontok százait tanulmányozta, majd arra jutott – nem hagyva helyet a minden tudományra jellemző kétségnek –, hogy az ishangói csont holdnaptár. Hisz az első két oszlop összege 60, azaz 2 holdhónap. A harmadik oszlop összege 48, azaz másfél holdhónap. A holdfázisokat a bevésések apró elhajlásai, vagy mélysége jelzik – ezek mikroszkóppal jól láthatók. Mindaz, amit az afrikai népekről tudunk, valamint a mikroszkopikus bizonyítási módszer gyengesége a hipotézist valószínűtlenné teszik. Ráadásul voltak és vannak sokkal jobb elméletek is.
Kőkorszaki logarléc
Vladimir Pletser, az Európai Űrügynökség parabolarepüléseinek vezetője, és Dirk Huylebrouck matematikus (Hogeschool, Brüsszel) 1999-ben a Tsukuba egyetem kongresszusán új értelmezéssel álltak elő. Pletser emlékeztetett a régi számológépekre: ezek 2-3, egymás mellett csúsztatható rovátkázott pálcából álltak, s gyors számoláshoz használták őket pl. mérnökök, matematikusok. Egyik pálcáról a másikra átlépve lehetett látni a kapcsolatot a két pálcán lévő számok közt. Éppígy az ishangói csonton! Itt a 3, 6, 4 a középső oszlopon található, összegük pedig, a 13 a mellette lévőn. Az 5, 5, 7 együtt 17, ez is egy szomszédos oszlopon szerepel. Ráadásul a bot könnyen kezelhető, egyik csoportról a másikra forgatni nyilvánvaló művelet. Így a tudósok szerint a csont olyan emberek munkája lehet, akik 10-es és 12-es (vagy 6-os) alapot használtak. Az ilyen értelmezés jobban megfelel az afrikai számolási módszereknek, hiszen itt ma is vannak népcsoportok, amelyek 12-es alapon számolnak.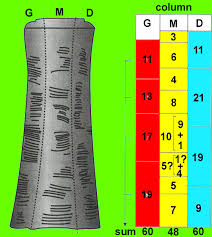 
A 12-es alapnak Európában is vannak maradványai: 1 év 12 hónap, 1 nap 2×12 óra, 1 óra 5×12 perc, a zodiákus 12 jelet tartalmaz. N. W. Thomas nyelvész még 1920-ban bukkant rá a nigériai yasguákra. Ők a számoknak 1-től 12-ig adtak külön nevet, majd a 13 12+1, a 14 12+2 és így tovább. Hasonlót Thomas csak Közép-Afrikában, a semliki völgyében talált – ez Ishangó vidéke is. Afrikában ugyan, mint nálunk, a 10-es alap az általános, de aritmetikai kreativitásuk más számolási módokban is megmutatkozik. Dél-Afrikában a 2-es alap egy változatát használják, másutt a 20-ast, 32-est, vagy éppen a 4-es és a 6-os keverékét. Azáltal, hogy egyre nagyobb sokféleséget látunk, a csont egyre kevésbé rejtélyes. Egyszerű számolási eszköz, amilyet Afrikában ezrével találni botokon, köteleken, köveken.
Emberevő számítások
Thomas ugyan 1920-ban még nem ismerhette az ishangói csontot, ennek ellenére felvetette, hogy kapcsolat lehet Nigéria, a semliki régió és Egyiptom között. Ezt a számnevek, a kultúra és a temetkezési szokások hasonlóságára alapozta. Mivel az egyiptomi számrendszer alapfeltétel volt a görög tudomány eredményeihez – és így számos más tudományos fejlődéshez –, lehet, hogy a mai világ, részben legalábbis, olyan népeknek adósa, amelyek ishangóban éltek. Akár így van, akár nem, figyelemre méltó, hogy a legrégebbi számrendszer-alkalmazás a középső kőkorszaki Közép-Afrikából származik. Európában semmilyen ásatás nem tárt fel hasonlót. Mire használhatták a számolást a hagyományos közösségek? Heinzelin szerint olyan aktív, nagy létszámú csoportokban éltek, ahol a szomszédokkal, ellenségekkel számos viszonyt le kellett rendezni. Javakat felosztani a családok között, figyelembe véve a halászat eredményeit, a gyerekek számát, az egyének rangját. Viszonozni azt, amit a vadászok és a halászok hoztak. Rabszolgákat, rabokat, ehető áldozatokat – sőt kockázatot és hasznot – elosztani. A viszonyok e rendezésének módját adták át generációról generációra, amihez szükség lehetett számolóbotra is. Mindez messze esik a történelem előtti vademberrel kapcsolatos elképzelésektől – ám tökéletesen megfelel a régészek ezen népek kultúrájával kapcsolatos mai, jócskán megváltozott nézeteinek.
Fekete Athén
Heinzelin követői szerint a matematika afrikai eredetű, és lényeges kapcsolat állt fenn Fekete-Afrika és Egyiptom között. Martin Bernal sinológus (Cambridge) úgy véli, a szubszaharai Afrika Görögországot is elérte (Black Athena, 1990). Egyiptomban igen ritka az ilyen vélemény, az USÁban pedig sokat vitatják, hogy az afrikaiak mennyire járultak hozzá a világ fejlődéséhez. Eközben az ishangói csont egyre híresebb. Angliában Ishango Science Clubok alakulnak, hogy afrikai bevándorlók gyermekeit támogassák a matematika-tanulásban. A belgák a matematika évére (2000) bélyeget adnak ki rovátkákkal (ezeket vonalkódnak vélni szerencsés tévedés: a matematika Ishangóban ilyen vonalakkal indult, ma a szupermarketek kódjai ehhez térnek vissza).
A Ruandában született belga filmrendező, Georges Kamanayo az ishangói csontról készítene etnomatematikai „dokudrámát”, hogy új képet fessen Afrikáról. Többé ne a nyomor, esetleg a sport, a zene, vagy a szép tájak asszociálódjanak csupán hozzá, hanem a matematika is. A filmre azonban még várni kell: Belgiumban egyszerűen nincsenek hívei az ügynek. Ha valaki szépen megkéri, annak megmutatják a csontot a Belga Természettudományi Múzeum XIX. emeletén – de ennyi. A tudománynak viszont el kell ismernie, hogy – akár túlzás a „fekete Athén”, akár nem –, a matematika „Termékeny Félholdban” történt kitalálását legalább tizenöt évezreddel előzte meg a számok megjelenése.
Beszélő fosszíliák
Távolodjunk el egy pillanatra a konkrétumoktól, a számolásra utaló leletektől és az ezzel kapcsolatos leleményektől. Kérdezzünk másképp. Nem azt, hogy mióta vannak nyomai a matematikai tevékenységnek, hanem, hogy elvileg mióta képes erre az ember. Mióta képes arra, hogy fogalmakat alkosson, ezekhez jeleket társítva? Tudjuk, bizonyos szinten az állatok is képesek rá, egyes példányok néhány számjelre is megtaníthatók, ahogy erről még lesz szó. De az elsajátítás nehézkes az emberhez viszonyítva, és maguktól az állatoknak nem sok késztetésük van ilyesmire. Mikortól válhatott a jelek, szimbólumok használata általánossá? A chauvet-i (Ardèche megye, Franciaország) barlangrajzok arra utalnak, hogy a Homo sapiens már 31 000 évvel ezelőtt komoly ábrázolási készséget mutatott fel.
Ami azonban a legérdekesebb, hogy az állatcsoportok rajzai mellett szimbólumok – például kereszt – is láthatók.
Mindez egyfajta kognitív modernséget sejtet. Az ennél korábbi őseinkkel nem sok mindenről tudtunk volna csevegni. Azokkal viszont, akik a lassú fejlődés folytán már rendelkeztek a szimbólumalkotás képességével, kis túlzással akár Einstein relativitáselméletéről is beszélgethettünk volna, persze, csak ha tanultak volna róla az iskolában. Ez persze fikció, amíg nincs tárgyi bizonyíték a kezünkben. Márpedig az időben visszafelé haladva, a kultúra nyomai ritkulnak. Hová forduljunk, ha az egyre távolabbi múltból már nem üzennek sem csontra vésett rovátkák, sem barlangi festmények? Kérdezzük magukat a hajdani embereket – ha nem is maradt fenn belőlük több mint egy-egy csontdarab. Ugyanis ha ezek a csontok koponyadarabok, merész paleoantropológusokat máris alapvető következtetésekre inspirálhatnak.
A kognitíve modern embernek ugyanis van egy különleges tulajdonsága: nagy agya csak nagy fejben fér el, ami azonban problémát jelentene a szülésnél. Így az embercsecsemő korábban jön világra, mint hogy agyának érése befejeződnék. Míg egy 13 éves csimpánz már felnőtt, az ember csak 20 éves kora felé az. Születési agytömege harmada a felnőttkorinak. Szemben például a makákó agyával, amely 1 éves korára eléri felnőttkori fejlettségét, az emberi agyat serdülésig alakítják a külvilág hatásai. Ez is magyarázza nagyfokú szellemi aktivitásunkat. A tudósnak tehát azt kell kikövetkeztetnie a koponyacsontokból, hogy azok hány éves emberektől származhattak. A gyerekeket összehasonlítva az ugyanakkor élt felnőttekkel pedig ki lehet deríteni, hány évet vett igénybe az adott hominida agyfejlődése.
Konkrétan: 2004-ben egy 1,6 millió éve élt Homo erectus gyermek fosszíliájának elemzéséből kiderült, hogy agyának mérete 1 éves korára már elérte a felnőttkorinak 80%-át. Vagyis a Homo erectus szellemi képességei messze nem érték el a mai szintet. És a Homo sapienséi? A legrégebbi gyermek Homo sapiens-lelet 160 ezer éves. 2007-ben Jean-Jacques Hublin (Max Planck Intézet, Lipcse) kimutatta, hogy ezen emberpalánta növekedési ritmusa megfelelt a mienknek. S ha úgy 150–200 ezer éve őseink agya ugyanolyan adottságokkal rendelkezett, mint a miénk, akkor nem bolondság azt képzelni, hogy az emberek – jóval a mezopotámiaiak előtt, jóval Ishango egykori lakosai előtt – folytathattak olyan tevékenységet, amely már egyfajta matematikával rokon. És fordítva…
A folytatás itt olvasható.
Kommentek
Kommenteléshez kérlek, jelentkezz be: