Írásom utolsó és szükségszerűen valamivel technikaibb részében azt szeretném megmutatni, mennyit veszíthetünk, ha a matematikai különböző részei közötti szakadékokat hagyjuk elmélyülni, és mennyit nyerhetünk, ha megpróbálunk föléjük hidakat verni.
Végtelen és véges
A matematikai gondolkodás egyik csúcsteljesítménye a végtelenség és folytonosság fogalmának megragadása. A halmazelmélet és analízis a matematika központi területei. A véges (diszkrét) matematika is kinőtt a fejtörők világából, és mint láttuk, sok alkalmazási terület fő eszköze lett. Mégis, a „folytonos” és „diszkrét” matematikát sok strukturális, módszertani és kulturális szakadék választja el. Talán fölösleges azzal érvelnem, hogy a diszkrét és a folytonos matematika kiegészítik egymást, kölcsönösen hasznosítják egymás módszereit és eszközeit.
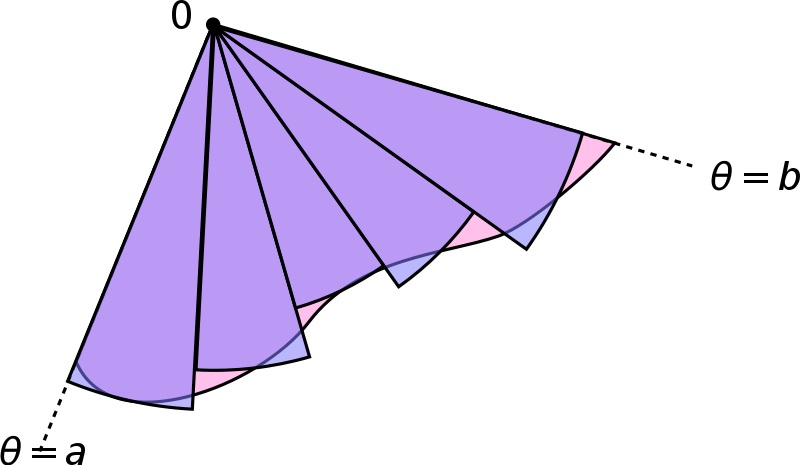 A végtelent például a végessel tudjuk megközelíteni. Bonyolult folytonos struktúrák „diszkretizálása” mindig is egy alapmódszer volt – a Riemann-integráltól kezdve a sokaság háromszögelésén át (például a homológiaelméletben), a parciális differenciálegyenletek rácson való numerikus megoldásáig.
A végtelent például a végessel tudjuk megközelíteni. Bonyolult folytonos struktúrák „diszkretizálása” mindig is egy alapmódszer volt – a Riemann-integráltól kezdve a sokaság háromszögelésén át (például a homológiaelméletben), a parciális differenciálegyenletek rácson való numerikus megoldásáig.
Ennek ellenére úgy gondolom, hogy a diszkrét matematika módszereinek alkalmazása a folytonos matematikában egyáltalán nem érte el azt a szintet, amit elérhetne. Ennek egyik oka talán az, hogy a kombinatorika nem érte még el az analízis vagy az algebra mélységét és erejét. Egy másik ok azonban lehet kulturális: egy diszkrét matematikus inkább tanult a Galois elméletről vagy a Borsuk-Ulam tételről, mint egy “klasszikus” matematikus például a Ramsey elméletről vagy a Maximalis-Folyam-Minimális-Vágás tételről (a fiatalok körében ez megváltozóban van, öröm látni, ahogy a legkiválóbbak egyforma természetességgel nyúlnak mindkét polcra eszközért).
Valamivel mélyebb gondolat, hogy a végtelen gyakran (vagy talán mindig?) a nagyon nagy véges közelítése.
A folytonos struktúrák gyakran tisztábbak, szimmetrikusabbak és gazdagabbak, mint diszkrét társaik (egy síkbeli rácsnak például sokkal kevesebb szimmetriája van, mint az egész euklidészi síknak). A diszkrét struktúrák “beágyazása” a folytonos világba egy természetes és jól használható módszer a tanulmányozásukra.
Ennek klasszikus példája a generátorfüggvények felhasználása (folytonos változóval) egy sorozat struktúrájának elemzésére. De más fontos példák is akadnak. A topológia például maga a folytonosság tudománya, annak megértésére született; mégis, az algebrai topológia módszereit is felhasználták már tisztán kombinatorikai állítás bizonyításához (lásd a [2] áttekintést).
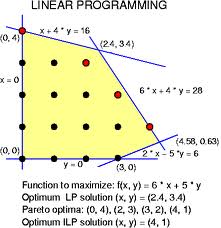 A hatvanas-hetvenes években a diszkrét optimalizáció egyik vezető témája a lineáris programozás módszereinek alkalmazása volt. A legfontosabb kombinatorikus optimalizációs problémák könnyen megfogalmazhatóak mint lineáris programozási problémák, azzal a mellékfeltétellel, hogy egészértékű megoldást keresünk. Ezeket könnyű is megoldani, ha az egész értékekre vonatkozó feltételt nem vesszük figyelembe; igazából arra megy ki a játék, hogyan lehet ezeket a lineáris programokat úgy felírni, hogy az egészértékűségi feltétel figyelmen kívül hagyása indokolt legyen, ne változtassa meg az eredményt.
A hatvanas-hetvenes években a diszkrét optimalizáció egyik vezető témája a lineáris programozás módszereinek alkalmazása volt. A legfontosabb kombinatorikus optimalizációs problémák könnyen megfogalmazhatóak mint lineáris programozási problémák, azzal a mellékfeltétellel, hogy egészértékű megoldást keresünk. Ezeket könnyű is megoldani, ha az egész értékekre vonatkozó feltételt nem vesszük figyelembe; igazából arra megy ki a játék, hogyan lehet ezeket a lineáris programokat úgy felírni, hogy az egészértékűségi feltétel figyelmen kívül hagyása indokolt legyen, ne változtassa meg az eredményt.
A máshonnan származó eszközök ereje
Hogy a matematika egységére irányuló igényemet alátámasszam, hadd említsem az algoritmuselmélet egy közelmúltbeli fejleményét. A kiinduló példa egy egyszerű, gráfelméletből vett algoritmikus probléma: legyen adott egy (véges) G gráf; osszuk be a ponthalmazát két osztályra oly módon, hogy az ezeket összekötő élek száma a lehető legnagyobb legyen. Bár egyszerűnek tűnik, ez egy meglehetősen fontos probléma.
Ez a feladat persze „elvileg” könnyen megoldható: nézzük végig az összes lehetséges kettéosztást, és válasszuk ki a legjobbat. Sajnos ez az egyszerű megoldás igen sok időt igényel: egy n pontú gráf pontjait 2^n módon lehet két osztályba osztani, ami már olyan viszonylag kis gráf esetén is, amikor n=10, csillagászati szám. Így minden kettéosztást végignézni gyakorlatilag lehetetlen. Olyan algoritmust keresünk ezért, melynek ez időigénye ennél sokkal kisebb. A számításelméletben az olyan algoritmust szokás hatékonynak tekinteni, melynek az időigénye növekvő gráf-méret esetén csak úgy növekszik, mint a pontszám egy hatványa (nem exponenciálisan, mint a fenti algoritmus esetén).
Már majdnem 30 éve bebizonyították, hogy ez a probléma NP-nehéz. Ez a technikai kifejezés körülbelül azt jelenti, hogy nincs hatékony (polinomidejű) módszer az optimális kettéosztás megtalálására (legalábbis ha elfogadjuk a bonyolultságelmélet alapvető hipotézisét, amit röviden úgy neveznek, hogy P=NP). Kevesebbel kell tehát beérnünk, mondjuk a közelítően optimális felosztás megtalálásával.
Nagyon könnyű olyan felosztást találni, ahol az éleknek legalább a fele a két osztály között megy; ezt először Erdős Pál vette észre a hatvanas években, egy egészen más kérdéssel kapcsolatban. (Egyszerűen vegyük sorra a pontokat, és mindegyiket helyezzük jobbra vagy balra aszerint, hogy melyik ad több keresztbe menő élt. Minden lépésnél az újonnan behozott éleknek legalább fele keresztbe megy.) Mivel egy felosztásnál a legjobb esetben se mehet több él keresztbe, mint az összes, így olyan közelítő megoldást kapunk, ami az optimumnak legalább 50 %-át eléri.
Tudunk-e ennél jobb arányt elérni? Ez az egészen ártatlan kérdés a közelmúltig megválaszolatlan volt, amikor, szinte egyidejűleg, két fontos eredmény született: Goemans és Williamson megadtak olyan hatékony algoritmust, aminek a hibája kisebb, mint 13 %; Hastad viszont azt bizonyította be, hogy nincs olyan hatékony közelítőalgoritmus, amelynek eredménye minden esetben 6 %-nál közelebb van az optimumhoz (pontosabban, NP-nehéz ilyen algoritmust találni).
Az algoritmusok elmélete igen nehéz terület, és az, hogy a legjobb elképzelhető hatékony közelítő algoritmus hibáját ilyen szűk határok közé sikerült szorítani, igen meglepő. A mi szempontunkból most azonban az a fontosabb, hogy mindkét eredményt váratlan helyről érkezett eszközökkel érték el (és amelyek ennek ellenére egy sor hasonló problémánál is alkalmazhatók).
A “negatív” eredmény mintájára egy sor más optimalizálási feladatról is bebizonyítható, hogy bizonyos korlátnál jobban még közelítően sem oldhatóak meg hatékonyan. Az első ilyen bizonyítást Feige, Goldwasser, Lovász, Safra és Szegedy adták, az ún. interaktív bizonyítási rendszerek egy alapvető eredményét (Babai, Fortnow és Lund) alkalmazva, ami a bonyolultságelmélet egy nagyon érdekes, de első ránézésre meglehetősen speciális területe. Később kiderült, hogy ebben a bizonyításban a legfontosabb matematikai konstrukció egy algebrai módszerekkel nyert hibajavító kód, tehát távoli rokona pl. annak az eljárásnak, amit a CD-lemezek használnak!
A “pozitív” eredmény, maga az algoritmus is egy sor korábbi eredményre épül, egymástól távol eső szakterületeket kapcsolva össze. A kulcslépés itt a szemidefinit optimalizáció használata, ami a lineáris programozás egy, a szimmetrikus mátrixok elméletére építő kiterjesztése. Ebben az esetben sem egy elszigetelt eredményről beszélünk, hiszen a szemidefinit optimalizációt ( véletlen algoritmusokkal kombinálva) sikerrel alkalmazták más közelítő algoritmusok tervezésében is.
Valószínűségelmélet
Ezzel egy olyan témához érkeztünk, ami talán a leggyakrabban játszik összekötő szerepet a matematika különböző szakterületei között. Robbanásszerűen nő a valószínűségszámítási módszerek fontossága a kombinatorikában, gráfelméletben és az algoritmusok elméletében.
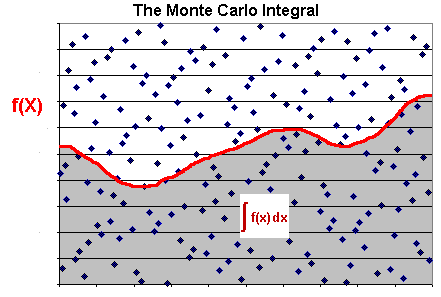
Az integrálás, szimuláció és véletlen algoritmusok u.n. Monte-Carlo-módszerében való hagyományos alkalmazásukon kívül használják még őket leszámlálásra, pontos és közelítő optimalizációra, prímtesztelésre, és még hosszan folytathatnám a sort.
A nem algoritmikus gráfelméletbe Erdős Pál (lásd pl. [1]) vezetett be valószínűségszámítási módszert az ötvenes években. Ennek alapgondolata az, hogy sokszor egy bizonyos, speciális tulajdonságokkal rendelkező struktúrát (gráfot, számsorozatot stb) nem tudunk megkonstruálni, de véletlenszerűen választva egy nagyobb osztályból, a kívánt tulajdonság nagy vaószínűséggel teljesülni fog.
Ez a fogás mostanra a gráfelmélet alapvető és jól működő eszközévé vált. A valószínűségszámítás olyan tételek bizonyításába került bele, amelyeknek látszólag semmi közük nincs hozzá. A valószínűségszámítás szerepe természetesen nem korlátozódik a kombinatorikára és gráfelméletre, hadd említsem például a szitamódszert a prímszámelméletben, vagy a turbulencia analízisét a hidrodinamikában [3].
Mélyebb egység
A valószínűségelmélet persze csak egyfajta illusztráció ahhoz, hogy a matematika egysége a más szakirányoktól származó eszközök használatánál jóval mélyebben gyökerezik. A legtöbb alapvető kérdés természete nem a priori diszkrét vagy folytonos – mind diszkrét, mind folytonos problémaként is lehet modellezni őket.
Az utóbbi években mintavételi algoritmusokkal foglalkoztam, amelyek egy véletlen elemet generálnak egy nagy és gyakran bonyolult halmazból. A kérdés a véletlen séták (Markov-láncok) keverési idejének becsléséhez vezet (hány lépést kell tenni, mielőtt a lánc alapvetően stacionárius lesz?). Az alkalmazás szempontjából a Markov láncokat végesnek természetes tekinteni – egy számítógép által végzett számítás szükségszerűen véges. Az elemzés során viszont a konkrét alkalmazástól függ, hogy az ember véges vagy általános, mérhető állapotteret akar használni. Az általános matematikai kérdés valójában a diszperzió: érdekelhet minket a hő diszperziója egy bizonyosfajta anyagban, egy véletlen séta során a valószínűség diszperziója vagy más hasonló kérdések. Mindig van egy “Laplace operátor”, amely a diszperzió egy lépését leírja. A diszperzió sebességét a Laplace operátor spektrális rése határozza meg, de ha a spektrális résről nincs információnk, akkor a diszperziós sebességet az állapottér izoperimetrikus egyenlőtlenségeinek segítségével is meg lehet becsülni. Az izoperimetrikus egyenlőtlenségek felállítására a leggyakrabban többtermékes folyamot kell (explicite vagy implicite) szerkeszteni. (A bekezdésben kevertem a hőtan klasszikus nyelvét a gráfelméletével, természetesen akarattal.)
A matematika felosztásának nincs természetes módja, de súlyos kommunikációs problémák alakulhatnak ki, ha nem vesszük figyelembe, hogy az egység megőrzésének költsége van. Nem csak a szervezésre kell időt áldozni, hanem a kutatási tevékenység egy részét ismertető írásra és ezek elolvasására kell fordítani, a matematika népszerűsítésére és arra, hogy meghallgatunk olyan matematikai problémákat, amik az elmélet vagy az alkalmazás különböző területein merülnek föl.
Irodalom
1. N. Alon and J. Spencer, The Probabilistic Method. With an Appendix
by Paul Erdős, Wiley, New York, 1992.
2. A. Björner, Topological methods, in: Handbook of Combinatorics
(eds. R.L.Graham, L.Lovász, M.Grötschel), Elsevier, Amsterdam, 1995,
1819–1872.
3. A.J. Chorin, Vorticity and turbulence , Springer, New York, 1994.
4. S. Fajtlowicz, On conjectures of Graffiti, Discrete Math.
72 (1988), 113–118.
5. P. Halmos, Applied mathematics is bad mathematics, in: Mathematics Tomorrow (ed. Lynn Arthur Steen), Springer-Verlag, New York, 1981.
6. L. Lovász, Algorithmic mathematics: an old aspect with a new emphasis, in: Proc. 6th International Congress on Math. Education, Budapest, 1988 , J. Bolyai Math. Soc., 1988, 67–78.

Kommentek
Kommenteléshez kérlek, jelentkezz be: